Question

A simple pendulum has a 100.0 g mass tied to it and 23.00 seconds are required to complete 10 oscillations.

(a) If g = 9.80 m/s^2, what is the length of the pendulum?
(b) When the mass is released from a certain hight, its speed as it passes through its lowest point is measured to be 1.620 m/s. Calculate the tension in the string at the pendulum's lowest point,
(c) When the 100.00 g mass is removed from the string forming the pendulum, it is attached to a spring. If 23.00 seconds is required to complete 25 oscillations on the spring, calculate the spring constant,
(d) If you are to move pendulum to another planet where g = 6.58 m/s^2, how will period change?
(e) If you are to move spring mass system to another planet where g = 6.58 m/s^2, how will period change. Please show detailed calculations.

Answer 1

a) The length of the pendulum is 1.31 m

b) The tension in the string is 1.18 N

c) The spring constant is 4.66 N/m

d) The period of the pendulum increases from 2.30 s to 2.80 s

e) The period of the spring does not change

Step-by-step explanation:

a)

The frequency of oscillation of the pendulum is

`f=(N)/(t)=(10)/(23.0)=0.435 Hz`

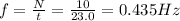
where N = 10 is the number of oscillations in a time of
`t=23.0 s`.

The period of a simple pendulum is given by

`T=2\pi \sqrt{(L)/(g)}`

where L is the length of the pendulum and g is the acceleration of gravity. Since the frequency is the reciprocal of the period,

`f=(1)/(T)=(1)/(2\pi) \sqrt{(g)/(L)}`

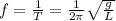
Since we know both f (the frequency) and g, we can solve the formula to find L, the length of the pendulum:

`L=(g)/((2\pi f)^2)=(9.80)/((2\pi (0.435))^2)=1.31 m`

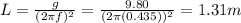
b)

The equation of motion for the pendulum when it passes through the lowest point is:

`T-W = F_c`

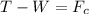
where

T is the tension in the string

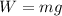`W=mg` is the weight of the pendulum, with
`m=100.0 g = 0.1 kg` being the mass of the pendulum and
`g=9.80 m/s^2`

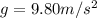
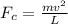`F_c = (mv^2)/(L)` is the centripetal force, where

m = 0.1 kg is the mass of the pendulum

v = 1.620 m/s is the speed at the lowest point

L = 1.31 m is the radius of the circular trajectory, which is the length of the pendulum

Substituting and solving for T, we find

`T=mg+(mv^2)/(L)=(0.1)(9.80)+((0.1)(1.620)^2)/(1.31)=1.18 N`

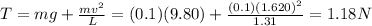
c)

The frequency of oscillation of the spring is:

`f=(N)/(t)=(25)/(23.0)=1.087 Hz`

where N = 25 is the number of oscillations in a time of
`t=23.0 s`.

The frequency of the spring can be written as

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

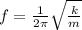
where

k is the spring constant

m = 0.1 kg is the mass attached to the spring

Since we know f and m, we can re-arrange the equation to find k, the spring constant:

`k=(2\pi f)^2 m = (2\pi (1.087))^2(0.1)=4.66 N/m`

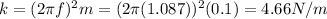
d)

The period of the a pendulum, as we said earlier, is given by

`T=2\pi \sqrt{(L)/(g)}`

where

L is the length of the pendulum

g is the acceleration of gravity

The length of this pendulum is

L = 1.31 m

On Earth,
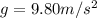`g=9.80 m/s^2`, so the period on Earth is

`T=2\pi \sqrt{(1.31)/(9.80)}=2.30 s`

Here the pendulum is moved to another planet, where the acceleration of gravity is

`g=6.58 m/s^2`

Substituting, we find the new period of the pendulum:

`T=2\pi \sqrt{(1.31)/(6.58)}=2.80 s`

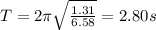
So, the period increases from 2.30 s to 2.80 s.

e)

The period of the spring is equal to the reciprocal of its frequency of oscillation:

`T=(1)/(f)`

We know that the frequency of oscillation is

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

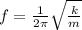
Therefore, we can write the period as

`T=2\pi \sqrt{(m)/(k)}`

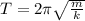
We see that the period does not depend on the value of g, the acceleration of gravity: therefore, if we move the spring on another planet, the value of its period does not change.