Answer:
number of revolutions = 5833.333
Step-by-step explanation:
The three equations for uniformly accelerated straight line motion are,
v = u + at
s = ut +
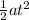
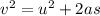
where,
v = final velocity
u = initial velocity
s = displacement
a = acceleration
These three equations can be applied to rotational motion also if the angular acceleration is constant just by replacing v with ω, u with ω₀, s with θ, and a with α.
where,
ω = final angular velocity
ω₀ = initial angular velocity
θ = angular displacement
α = angular acceleration
thus, the above equations become,
ω = ω₀ + αt
θ = ut +
 α
α
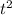
ω
 = ω₀
= ω₀
 + 2αθ
+ 2αθ
In the given problem,
initial angular velocity is ω₀ = 0 (since it starts from rest)
final angular velocity is ω = 350000 rpm = 350000 x
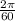 radian/sec =
radian/sec =
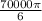 radian/sec
radian/sec
(since 0ne revolution = 2π radian and one minute = 60 seconds)
time t = 2.0 s
our aim is to find θ. We have two equations with θ. But both of them contains α which is an unknown. So we have to first find α using the first equation.
ω = ω₀ + αt
α = ( ω-ω₀)/t (got by finding α from the above equation.)
Substituting the known values in the equation we get,
α = ( ω-ω₀)/t
α =

α =
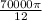 radian/
radian/
We know,
ω
 = ω₀
= ω₀
 + 2αθ
+ 2αθ
rearranging to find θ
θ = (ω^2 - ω₀^2)/2α
=
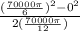
=
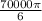 radian
radian
but we have to find number of revolutions. We know that one revolution = 2π radian
so to find the number of revolutions we have to divide the answer by 2π.
that is number of revolutions =
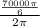 revolutions
revolutions
=
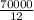 revolutions = 5833.333 revolutions
revolutions = 5833.333 revolutions