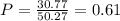Question

Can anyone please help me this? stuck with this problem for hours

Answer 1

P=0.61 or 61%

Explanation:

If we pick a random point within the circle, it can fall in the white area or in the pink area. Since the sum of both areas makes the sample space or the total area of the circle, we can compute the probabilities according to the ratio of the areas with respect to the total area, that is:

`\text {Probability of falling in the white area} = \frac{\text{White area}}{\text{Circle area}}`

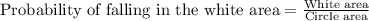
The area of the circle is

`A_c=\pi r^2`

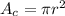
The area of both the triangles is

`A_t=2*(bh)/(2)`

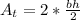
Where r=4 cm, b=3 cm, h= (4+2.5) cm = 6.5 cm

Then we have:

`A_c=\pi 4^2=16\pi \ cm^2=50.27\ cm^2`

`A_t=19.5\ cm^2`

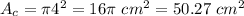
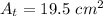
The white area is obtained by subtracting both areas

`A_w=A_c-A_t=50.27-19.5=30.77\ cm^2`

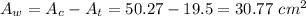
So the probability is

`P=(30.77)/(50.27)=0.61`