Answer:
m∠U=11°
Explanation:
we know that
The sum of the interior angles in a triangle must be equal to 180 degrees
so
In this problem
m∠U+m∠V+m∠W=180°
substitute the given values
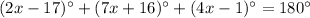
solve for x
Combine like terns left side
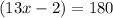
Adds 2 both sides
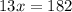
divide by 13 both sides
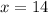
Find the measure of angle U
m∠U = (2x-17)°
substitute the value of x
m∠U = (2(14)-17)=11°