Question

an aeroplane flies in a direction 60 north at East then 30km straight East 10 km straight north find magnitude and direction of resultant displacement​

Answer 1

Question:

An air plane flies 20 km in a direction 60 degrees north of east, then 30 km straight east, then 10 km straight north. find magnitude and direction of resultant displacement​.

Answer:

34.33 degree north of east is the direction of resultant displacement​ and 27.32 km , its magnitude.

Step-by-step explanation:

Let us consider,

An aero plane in a Northern component at 60 degrees = sin (60)

An aero plane in a Eastern component at 60 degrees = cos (60) Find the x-coordinate at point C,

`x=O A \cos \theta+A B=20\left(\cos 60^(\circ)\right)+30=20(0.5)+30=10+30=40 \mathrm{km}`

Find the y-coordinate at point C,

`y=O A \sin \theta+B C=20\left(\sin 60^(\circ)\right)+10=20(0.866)+10=17.32+10=27.32 \mathrm{km}`

Now, displacement,
`D=\sqrt{x^(2)+y^(2)}=\sqrt{40^(2)+27.32^(2)}=√(1600+746.38)=√(2346.38)=48.439 \mathrm{km}`

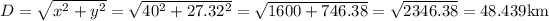
To find direction,

`\tan \varphi=(y)/(x)=(27.32)/(40)=0.683`

`\varphi=\tan ^(-1)(0.683)=34.33^(\circ)`

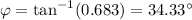
So, 34.33 degree north of east compared to the starting location.