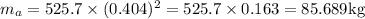Question

A 22.5 kg chair attached to a spring takes 1.30 s to complete one cycle of oscillation. With an astronaut sitting in the oscillating chair with feet off the floor, a full oscillation cycle takes 2.54 s. What is the astronaut's mass?

Answer 1

85.689 kg is the astronaut's mass.

Step-by-step explanation:

Given data: m = 22.5 kg and T = 1.3 sec

So, using the below formula,

`T = 2 \pi \sqrt{(m)/(k)}`

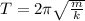
Now, after putting the values of m and T in the above equation, we will find out the value of k which is as,

`1.3 = 2 *\left((22)/(7)\right) \sqrt{(22.5)/(k)}`

`1.3 * 7=44 \sqrt{(22.5)/(k)}`

`(9.1)/(44)=\sqrt{(22.5)/(k)}`

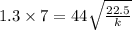
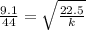
To remove the square root, take square on both sides, we get,

`(0.2068)^(2)=(22.5)/(k)`

`k=(22.5)/(0.0428)=525.7 \mathrm{N} / \mathrm{m}`

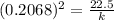
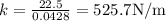
Now, we have the same string but this time we have different mass and different time. So, let the mass of the astronaut is
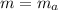`m=m_(a)` and
`T_(a)` = 2.54 sec, k= 525.7 kg. Apply these values in the equation, we get,

`2.54 = 2 * 3.14\left((m_(a))/(525.7)\right)^{(1)/(2)}`

`(2.54)/(6.28) = \left((m_(a))/(525.7)\right)^{(1)/(2)}`

`0.404 = \left((m_(a))/(525.7)\right)^{(1)/(2)}`

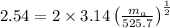
Taking squares on both sides, we get,

`m_(a) = 525.7 *(0.404)^(2)=525.7 * 0.163 = 85.689 \mathrm{kg}`