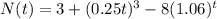Answer: D .
Explanation:
Given : Jenny studied the characteristics of two species of bacteria. The number of bacteria of species A, A(t), after t hours is represented by the function,

The number of bacteria of species B, B(t), after t hours is represented by the function,

Then, the difference in the number of bacteria, N(t), of both the species after t hours will be :-
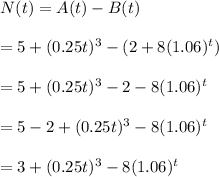
Hence, the correct answer should be : D .