The function f(x) =
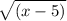 is undefined for all real numbers x that are less than 5. This includes all negative numbers, zero, and any fraction or irrational number whose value is less than 5.
is undefined for all real numbers x that are less than 5. This includes all negative numbers, zero, and any fraction or irrational number whose value is less than 5.
The function f(x) =
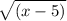 defines the square root of the difference between the input value x and the constant 5. Since a square root always returns a non-negative number, the expression under the radical, x - 5, must be non-negative for the function to be defined at any input value x. This means that the radicand, x - 5, cannot be less than zero.
defines the square root of the difference between the input value x and the constant 5. Since a square root always returns a non-negative number, the expression under the radical, x - 5, must be non-negative for the function to be defined at any input value x. This means that the radicand, x - 5, cannot be less than zero.
To determine the values of x where the function is undefined, we set the radicand equal to zero and solve the resulting inequality:
x - 5 = 0
Solving for x, we get:
x = 5
Therefore, the function f(x) =
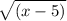 is undefined for all real numbers x that are less than 5. This includes all negative numbers, zero, and any fraction or irrational number whose value is less than 5.
is undefined for all real numbers x that are less than 5. This includes all negative numbers, zero, and any fraction or irrational number whose value is less than 5.
Complete question below:
Consider the function f(x) =
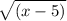 . For which values of x is f(x) undefined?
. For which values of x is f(x) undefined?