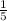Question

An exponential function in the form y=500(b)x contains the points (0,500) and (3,4). What is the value of b?

Answer 1

1/5

Explanation:

Substitute the point (3,4) into the equation y=500(b)x to find the value of b.

41125=b3(15)3=500(b)3=b3

The value of b is 15.

Answer 2

An exponential function in the form y=500(b)^x contains the points (0,500) and (3,4). What is the value of b?

Answer:

An exponential function in the form y=500(b)^x contains the points (0,500) and (3,4). Then the value of b is
`(1)/(5)`

Solution:

Given that, An exponential function in the form
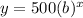`y=500(b)^(x)` contains the points (0,500) and (3,4).

We have to find what is the value of b

Now, as the function contains (0, 500), let us substitute it in given function.

`\begin{array}{l}{\rightarrow \quad 500=500 * \mathrm{b}^(0)} \\\\ {\rightarrow \quad 1=\mathrm{b}^(0)}\end{array}`

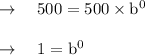
Here, it is not possible to find b exact value, as anything power 0 is 1.

So, now let us go for the next point. i.e. (x, y) = (3, 4)

Substitute x = 3 in given function

`\begin{array}{l}{4=500 * b^(3)} \\\\ {1=125 * b^(3)} \\\\ {1=5^(3) * b^(3)}\end{array}`

`\begin{array}{l}{1=(5 b)^(3)} \\\\ {(5 b)^(3)=1^(3)} \\\\ {5 b=1} \\\\ {b=(1)/(5)}\end{array}`

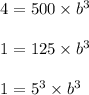
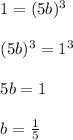
Hence, the value of b is
`(1)/(5)`