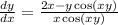Question

If sin(xy) = x^2, then dy/dx= ?

Show all work

Answer 1

Step-by-step explanation:

`\sin(xy)=x^2`

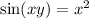
We want to differentiate both sides since we are to find
`(dy)/(dx)`.

`(\sin(xy))'=(x^2)'`

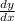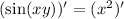
The right hand side is easy and is one step. You apply the power rule on the right hand side. The side that is going to be a little hard is the left hand side.

So let's focus on that for now.

`(\sin(xy))'`

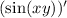
We will begin with chain rule:

`(xy)'\cos(xy)`

Now we must use the product rule to differentiate the
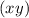`(xy)` part:

`(xy'+1y)\cos(xy)`

`(xy'+y)\cos(xy)`

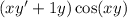
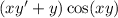
Distribute:

`xy'\cos(xy)+y\cos(xy)`

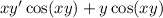
So we are done differentiate the left hand side.

The right hand side after applying power rule gives us
`(x^2)'=2x`.

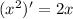Let's put it together:

`xy'\cos(xy)+y\cos(xy)=2x`

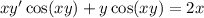
We need to get the term(s) with
`y'` alone. There is only one of these luckily. So moving the one term of
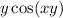`y\cos(xy)` to the other side will give us victory in getting the term with
`y'` alone.

`xy'\cos(xy)+y\cos(xy)=2x`

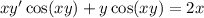
Subtracting
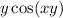`y\cos(xy)` on both sides gives:

`xy'\cos(xy)=2x-y\cos(xy)`

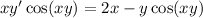
Dividing both sides by
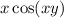`x\cos(xy)` gives:

`y'=(2x-y\cos(xy))/(x\cos(xy))`

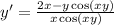
We could write
`y'` as
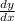`(dy)/(dx)` giving us:

`(dy)/(dx)=(2x-y\cos(xy))/(x\cos(xy))`