Question

Select the correct answer.

The vertex of a parabola is at the point (3.1), and its focus is at (3.5), what function does the graph represent?

A. f(x) = 1/16(x - 3)² - 1
B. f(x) = 1/4(x + 3)² - 1
C. f(x) = 1/4(x - 3)² - 1
D. f(x) = 1/16(x - 3)² + 1​

Answer 1

`y = (1)/(16) (x - 3)^(2) + 1`

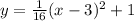
Explanation:

The vertex of the parabola is at the point (3,1) and its focus is at (3,5).

Therefore, the axis of the parabola is x = 3 and the direction is positive y-axis.

{Since focus is above the vertex.}

Therefore, the equation of the parabola can be written as

(x - 3)² = 4a(y - 1)

Where, a is the length between vertex and the focus which is (5 - 1) = 4

{Length is measured along x = 3 line}

So, the final equation of the parabola is (x - 3)² = 4 × 4(y - 1) = 16(y -1)

Now, rearranging the equation we get,

`y = (1)/(16) (x - 3)^(2) + 1`

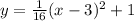
Therefore, option D is correct. (Answer)