Question

3. Maverick and Goose are flying a training mission in their F-14. They are

flying at an altitude of 1500. m and are traveling at 688 m/s (mach 2). They
release their bomb and head for home.

A. How long will it be before the bomb hits the ground

B . How far ( on the ground ) from where they released it will it land ?

Answer 1

A. The bomb will take 17.5 seconds to hit the ground

B. The bomb will land 12040 meters on the ground ahead from where they released it

Step-by-step explanation:

Maverick and Goose are flying at an initial height of
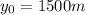`y_0=1500m`, and their speed is v=688 m/s

When they release the bomb, it will initially have the same height and speed as the plane. Then it will describe a free fall horizontal movement

The equation for the height y with respect to ground in a horizontal movement (no friction) is

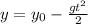`y=y_0 - (gt^2)/(2)` [1]

With g equal to the acceleration of gravity of our planet and t the time measured with respect to the moment the bomb was released

The height will be zero when the bomb lands on ground, so if we set y=0 we can find the flight time

The range (horizontal displacement) of the bomb x is

`x = v.t` [2]

Since the bomb won't have any friction, its horizontal component of the speed won't change. We need to find t from the equation [1] and replace it in equation [2]:

Setting y=0 and isolating t we get

`t=\sqrt{(2y_0)/(g)}`

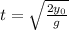
Since we have
`y_0=1500m`

`t=\sqrt{(2(1500))/(9.8)}`

`t=17.5 sec`

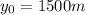
Replacing in [2]

`x = 688\ m/sec \ (17.5sec)`

`x = 12040\ m`

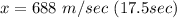
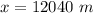
A. The bomb will take 17.5 seconds to hit the ground

B. The bomb will land 12040 meters on the ground ahead from where they released it