Question

(1.) Using Beer's Law, How will the absorbance measured for the solutions change as the concentration of aspirin in solutions increase?

(2.) In an experiment, the Beer’s Law plot resulted in the following relationship between absorbance and concentration of ASA, y = 1061.5x, where y is absorbance and x is the concentration. If the absorbance of a sample solution prepared from an aspirin tablet is 0.402, calculate the concentration of ASA in the solution in M.
(3.) If the above solution was prepared by taking 10 mL of stock solution and diluting it to 100 mL, what is the concentration of the stock solution?
(4.) This stock solution was prepared as follows: An aspirin tablet was transferred to an Erlenmeyer flask and reacted with NaOH. The resulting solution was transferred to a 250 mL volumetric flask and the volume made up to 250 mL. Calculate the mass of aspirin in the tablet based on the concentration of aspirin in the stock solution.

Answer 1

According to Beer's Law, as the concentration of aspirin in a solution increases, the absorbance measured will also increase. Using the given Beer's Law plot, the concentration of ASA in a solution with an absorbance of 0.402 is calculated to be 0.000378 M. The concentration of the stock solution is found to be 0.0000378 M, and the mass of aspirin in the tablet can be calculated as 0.00945 grams.

Step-by-step explanation:

According to Beer's Law, the absorbance of a solution is directly proportional to the concentration of the absorbing species in the solution. As the concentration of aspirin in a solution increases, the absorbance measured will also increase. This relationship is linear, meaning that if the concentration doubles, the absorbance will also double.

In the given Beer's Law plot, the relationship between absorbance and concentration of ASA is given as y = 1061.5x, where y is the absorbance and x is the concentration. To calculate the concentration of ASA in the solution with an absorbance of 0.402, we can rearrange the equation to solve for x: x = y/1061.5. Plugging in the absorbance value, we get x = 0.402/1061.5 = 0.000378 M.

The 10 mL of the stock solution was diluted to 100 mL, resulting in a dilution factor of 100/10 = 10. To find the concentration of the stock solution, we can divide the concentration of the diluted solution by the dilution factor: concentration of stock solution = concentration of diluted solution / dilution factor = 0.000378 M / 10 = 0.0000378 M.

Finally, to calculate the mass of aspirin in the tablet based on the concentration of aspirin in the stock solution, we need to know the volume of the stock solution used to prepare the tablet solution. Assuming the entire 250 mL of stock solution was used, we can use the formula: mass of aspirin = concentration of aspirin in stock solution * volume of stock solution = 0.0000378 M * 0.250 L = 0.00945 grams.

Answer 2

(1) The absorbance of the aspirin in solutions will increase.

(2) [ASA]f = 3.79x10⁻⁴M

(3) [ASA]i = 3.79x10⁻³M

(4) m ASA = 0.171g

Step-by-step explanation:

The Beer's Law is expressed by:

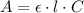`A = \epsilon \cdot l \cdot C` (1)

where A: is the absorbance of the species, ε: is the molar attenuation coefficient, l: is the pathlength and C: is the concentration of the species

(1) From equation (1), the relation between the absorbance of the species and its concentration is directly proportional, so if the aspirin concentration in solutions increases, the absorbance of the solutions will also increase.

(2) Starting in the given expression for the relationship between absorbance and concentration of ASA, we can calculate its concentration in the solution:

`A = 1061.5 \cdot [ASA]`

`[ASA] = (A)/(1061.5) = 3.79 \cdot 10^(-4)M`

Therefore, the aspirin concentration in the solution is 3.79x10⁻⁴ M

(3) To calculate the stock solution concentration, we can use the next equation:

`V_(i) [ASA]_(i) = V_(f) [ASA]_(f)`

where Vi: is the stock solution volume=10mL, Vf: is the solution diluted volume=100mL, [ASA]i: is the aspirin concentration of the stock solution and [ASA]f: is the aspirin concentration of the diluted solution

`[ASA]_(i) = (V_(f) \cdot [ASA]_(f))/(V_(i)) = \frac {100mL \cdot 3.79\cdot 10^(-4) M}{10mL} = 3.79 \cdot 10^(-3) M`

Hence, the concentration of the stock solution is 3.79x10⁻³M

(4) To determine the aspirin mass in the tablet, we need to use the following equation:

`m_(ASA) = \eta_(ASA) \cdot M_(ASA) = [ASA]_(i) \cdot V_(0) \cdot M_(ASA)`

where η: is the aspirin moles = [ASA]i V₀, M: is the molar mass of aspirin=180.158g/mol, V₀: is the volume of the volumetric flask=250mL and [ASA]i: is the aspirin concentration in the volumetric flask which is equal to the stock solution=3.79x10⁻³M

`m_(ASA) = 3.79 \cdot 10^(-3) (mol)/(L) \cdot 0.250L \cdot 180.158 (g)/(mol) = 0.171 g`

Then, the aspirin mass in the tablet is 0.171 g.

I hope it helps you!