Answer with Step-by-step explanation:
We are given that
M is the mid point of AB

We have to match the reasons with statements given in proof.
Proof:
1.Statement:
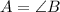 , M is the midpoint of AB
, M is the midpoint of AB
Reason: Given
2.Statement:

Reason: Definition of midpoint
3.Statement:

Reason:Opposite sides of equal angle are equal.
4.Statement:

Reason:SAS Postulate