Question

One of the same-side exterior angles formed by two lines and a transversal is equal to 1/6 of the right angle and is 11 times smaller than the other angle. Prove that the lines are parallel.

Answer 1

One of the same-side exterior angles formed by two lines and a transversal is equal to 1/6 of the right angle and is 11 times smaller than the other angle. Then the lines are parallel

Solution:

Given that, One of the same-side exterior angles formed by two lines and a transversal is equal to 1/6 of the right angle and is 11 times smaller than the other angle.

We have to prove that the lines are parallel.

If they are parallel, sum of the described angles should be equal to 180 as they are same side exterior angles.

Now, the 1st angle will be 1/6 of right angle is given as:

`\begin{array}{l}{\rightarrow 1^{\text {st }} \text { angle }=(1)/(6) * 90} \\\\ {\rightarrow 1^{\text {st }} \text { angle }=15 \text { degrees }}\end{array}`

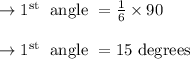
And now, 15 degrees is 11 times smaller than the other

Then other angle = 11 times of 15 degrees

`\text {Other angle }=11 * 15=165 \text { degrees }`

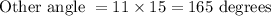
Now, sum of angles = 15 + 165 = 180 degrees.

As we expected their sum is 180 degrees. So the lines are parallel.

Hence, the given lines are parallel