Question

A generator produces 2 MW of electric power at 15 kV. The current is sent to a town 30 km away through aluminum transmission wires (resistivity 2.7 x 10-8 LaTeX: \Omega\cdot mΩ ⋅ m) with a diameter of 6.8 mm. What % of the electric power is lost during transmission?

Answer 1

To solve this problem it is necessary to apply the concepts related to Power in function of the current and the resistance.

By definition there are two ways to express power

`P = I^2R`

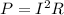
P =VI

Where,

P = Power

I = Current

R = Resistance

V = Voltage

In our data we have the value for resistivity and not the Resistance, then

`R = \rho (1)/(A)`

`R = 2.7*10^(-8)(1)/(\pi r^2)`

`R = 2.7*10^(8)(1)/(\pi (6.8*10^-3)^2)`

`R = 1.85*10^(-4)\Omega`

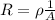
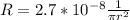
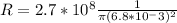
The loss of the potential can mainly be given by the resistance of the cables, that is,

`I = (P)/(V)`

`I = (2*10^6W)/(15*10^3V)`

`I = 133.3A`

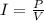
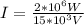
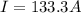
Therefore the expression for power loss due to resistance is,

`P = I^2 R`

`P = 133.3^2 * 1.85*10^(-4)`

`P_l = 3.2872W`

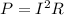
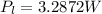
The total produced is
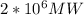`2 * 10 ^ 6 MW`, that is to say 100%, therefore 3.2872W is equivalent to,

`x = (3.2872*100)/(2*10^6)`

`x = 1.6436*10^(-4)\%`

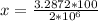
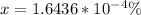
Therefore the percentage of lost Power is equivalent to
`1.6436 * 10 ^ 4 \%` of the total