Answer:
K = 80.75 MeV
Step-by-step explanation:
To calculate the kinetic energy of the antiproton we need to use conservation of energy:
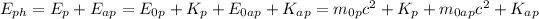
where
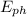 : is the photon energy,
: is the photon energy,
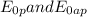 : are the rest energies of the proton and the antiproton, respectively, equals to m₀c²,
: are the rest energies of the proton and the antiproton, respectively, equals to m₀c²,
 : are the kinetic energies of the proton and the antiproton, respectively, c: speed of light, and m₀: rest mass.
: are the kinetic energies of the proton and the antiproton, respectively, c: speed of light, and m₀: rest mass.
Therefore the kinetic energy of the antiproton is:
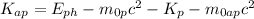
The proton mass is equal to the antiproton mass, so:
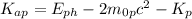
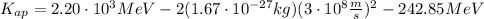
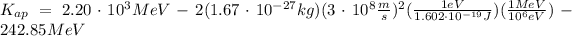
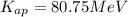
Hence, the kinetic energy of the antiproton is 80.75 MeV.
I hope it helps you!