Answer:
About 20.81 years
Explanation:
89 million is the "final population" -- population after t years.
So, 89 million would be in "A" in the equation. Then we will have to solve for "t" by taking LN (natural logarithm). That is how we solve exponential equations.
So,
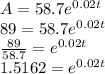
Now we recognize the exponential rule of:
Ln(e) = 1
and we use the property:
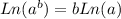
Now, we solve by taking Ln of both sides:
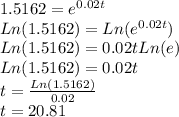
So, population would be 89 million in about 20.81 years