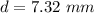Question

A cylindrical rod of copper (E = 110 GPa, 16 × 106 psi) having a yield strength of 240 MPa (35,000 psi) is to be subjected to a load of 6640 N (1493 lbf). If the length of the rod is 370 mm (14.57 in.), what must be the diameter to allow an elongation of 0.53 mm (0.02087 in.)?

Answer 1

`d=7.32\ mm`

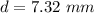
Step-by-step explanation:

Given:

• Young's modulus,
  `E=110* 10^3\ MPa`

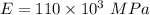
• yield strength,
  `\sigma_y=240\ MPa`

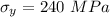
• load applied,
  `F=6640\ N`

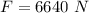
• initial length of rod,
  `l=370\ mm`

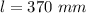
• elongation allowed,
  `\Delta l=0.53`

We know,

Stress:

`\sigma=(F)/(A)`

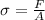
where: A = cross sectional area

Strain:

`\epsilon = (\Delta l)/(l)`

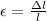
& by Hooke's Law within the elastic limits:

`E=(\sigma)/(\epsilon)`

`\therefore 110* 10^3=(F)/(A)/ (\Delta l)/(l)`

`\therefore 110* 10^3=(6640* 4)/(\pi.d^2)/ (0.53)/(370)`

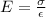
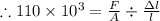
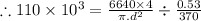
where: d = diameter of the copper rod

`d=7.32\ mm`

Answer 2

d= 7.32 mm

Step-by-step explanation:

Given that

E= 110 GPa

σ = 240 MPa

P= 6640 N

L= 370 mm

ΔL = 0.53

Area A= πr²

We know that elongation due to load given as

`\Delta L=(PL)/(AE)`

`A=(PL)/(\Delta LE)`

`A=(6640* 370)/(0.53* 110* 10^3)`

A= 42.14 mm²

πr² = 42.14 mm²

r=3.66 mm

diameter ,d= 2r

d= 7.32 mm