Answer:

Explanation:
SO for the total baggage weights onboard to exceed the 6000lb limit, with n = 100 passengers. Each of the passenger must exceed the weigh allowance of 6000/100 = 60lb limit as well.
The probability of that to happen with normal distribution of 48lb and standard deviation of 22lb is:
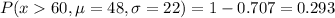
For all 100 passengers to exceed this limit, the probability for that to happen is
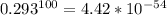
which is very low