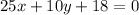Question

A rectangle is drawn on a coordinate grid. The equation for one side of the rectangle is 2x – 5y = 9. Which could be the equation of another side of the rectangle?

Answer 1

y=2/5x-9

I just answered this and got it right.

Explanation:

Answer 2

`25x+10y+18=0`

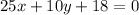
Explanation:

We are given that a rectangle in which the equation of one side is given by

`2x-5y=9`

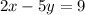
We have to find the equation of another side of the rectangle.

We know that the adjacent sides of rectangle are perpendicular to each other.

Differentiate the given equation w.r.t.x

`2-5(dy)/(dx)=0` (
`(dx^n)/(dx)=nx^(n-1)`)

`5(dy)/(dx)=2`

`(dy)/(dx)=(2)/(5)`

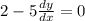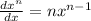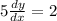
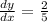
Slope of the given side=
`m_1=(2)/(5)`

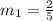
When two lines are perpendicular then

Slope of one line=
`-(1)/(Slope\;of\;another\;line)`

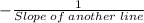
Slope of another side=
`-(5)/(2)`

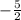
Substitute x=0 in given equation

`2(0)-5y=9`

`-5y=9`

`y=-(9)/(5)`

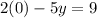
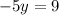
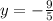
The equation of given side is passing through the point (
`0,-(9)/(5))`.

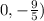The equation of line passing through the point
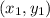`(x_1,y_1)` with slope m is given by

`y-y_1=m(x-x_1)`

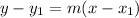
Substitute the values then we get

`y+(9)/(5)=-(5)/(2)(x-0)=-(5)/(2)x`

`y=-(5)/(2)x-(9)/(5)`

`y=(-25x-18)/(10)`

`10y=-25x-18`

`25x+10y+18=0`

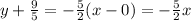
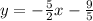
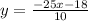
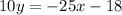
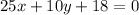
Hence, the equation of another side of rectangle is given by

`25x+10y+18=0`