Answer:
Option C.
Explanation:
Given information: RSTU is a parallelogram, Digonals RT and SU intersect each other at point V, UV=(x-3) and VS=(3x-13).
According to the properties of a parallelogram, the diagonals of a parallelogram bisect each other.
Using the properties of parallelogram we can say that point V divides the diagonal SU in two equal parts, UV and VS.
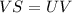
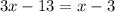
Subtract x from both sides.

Add 13 on both sides.
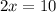
Divide both sides by 2.

Therefore, the correct option is C.