Answer:
1.25377 m/s²
Step-by-step explanation:
m = Mass of person
g = Acceleration due to gravity = 9.81 m/s²
 = Coefficient of friction
= Coefficient of friction
 = Slope
= Slope
From Newton's second law
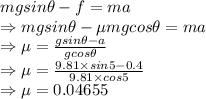
Applying
 to the above equation and
to the above equation and
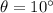
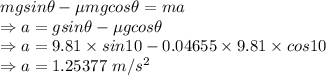
The acceleration of the same skier when she is moving down a hill is 1.25377 m/s²