Question

Two solenoids are nested coaxially such that their magnetic fields point in opposite directions. Treat the solenoids as ideal. The outer one has a radius of 20 mm, and the radius of the inner solenoid is 10 mm. The length, number of turns, and current of the outer solenoid are, respectively, 21.3 cm, 525 turns, and 5.89 A. For the inner solenoid the corresponding quantities are 18.1 cm, 317 turns, and 1.57 A. At what speed, v1, should a proton be traveling, inside the apparatus and perpendicular to the magnetic field, if it is to orbit the axis of the solenoids at a radius of 6.79 mm? v1=

Answer 1

To solve this problem it is necessary to apply the concepts related to the magnetic field of a body and the magnetic force.

By definition we know that the magnetic field is given by the equation

`B = (\mu_0 N I)/(L)`

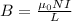
Where,

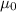`\mu_0` = Permeability constant at free space

N= Number of loops

I = Current

L = length

According to the information the two solenoids generate a unique magnetic field therefore

`B = B_1 + B_2`

`B = (\mu_0 N_1 I_1)/(L_1) - (\mu_0 N_2 I_2)/(L_2)`

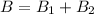
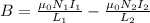
Replacing with our values we have that

`B = ((4\pi *10^(-7))(525)(5.39))/(0.213) - ((4\pi *10^(-7))(317)(1.57))/(0.181)`

`B = 0.0132T`

From this point we know that the centripetal force is equivalent to the magnetic force, therefore

`F_c = (mv^2)/(R)`

Where,

m=mass (proton)

v= velocity

r =Radius

`F_q = qvB`

Where,

q= Charge of electron

v = Velocity

B= Magnetic Field

Equation both equations,

`(mv^2)/(R) = q v B`

Re-arrange to find v,

`v = (R q B)/(m)`

`v= ((6.79*10^(-3))(1.6*10^(-19))(0.0132))/(1.67*10^(-27))`

`v = 8587.11 m/s`

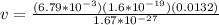
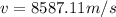
Therefore the speed is 8587.11 m/s