Question

A gyroscope slows from an initial rate of 53.3 rad/s at a rate of 0.736 rad/s2. How long does it take (in s) to come to rest?

Answer 1

72.42 seconds

Step-by-step explanation:

initial angular velocity, ωo = 53.3 rad/s

angular acceleration, α = - 0.736 rad/s

final angular velocity, ω = 0

Let the time taken is t.

Use first equation of motion

ω = ωo + αt

0 = 53.3 - 0.736 x t

t = 72.42 seconds

Answer 2

Time, t = 72.41 seconds

Step-by-step explanation:

It is given that,

Initial speed of the gyroscope, u = 53.3 rad/s

Finally, it comes to rest, v = 0

Acceleration of gyroscope,
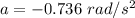`a=-0.736\ rad/s^2` (slows down)

Let t is the time taken by the gyroscope to come to a rest. Using the first equation of motion as :

`v=u+at`

`t=(v-u)/(a)`

`t=(-53.3\ rad/s)/(-0.736\ rad/s^2)`

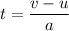
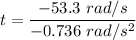
t = 72.41 seconds

So, the gyroscope takes 72.41 seconds. Hence, this is the required solution.