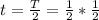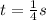To solve the problem it is necessary to identify the equation in the manner given above.
This equation corresponds to the displacement of a body under the principle of simple harmonic movement.
Where,

PART A) Our equation corresponds to
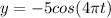
Therefore the value of omega is equivalent to that of
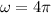
From the definition we know that the period as a function of angular velocity is equivalent to

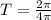
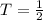
This same point is the equivalent of the maximum point of the speed that the body can reach, since the internal expression of the
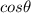 Is equivalent to . So the maximum speed that the body can reach is,
Is equivalent to . So the maximum speed that the body can reach is,
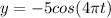
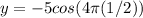
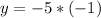
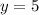
Therefore the maximum felocity will be 5ft / s
PART B) The period of graph is the time taken to reach from one maximum point to next point maximum point, then