Question

Find the absolute maximum and absolute minimum values of f on the given interval.

a) f(t)= t sqrt(36-t^2) [-1,6]
absolute max=
absolute min=
b) f(t)= 2 cos t + sin 2t [0,pi/2]
absolute max=
absolute min=

Answer 1

absolute max= (4.243,18)

absolute min =(-1,-5.916)

absolute max=(pi/6, 2.598)

absolute min = (pi/2,0)

Explanation:

a)
`f(t) = t√(36-t^2) \\`

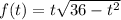
To find max and minima in the given interval let us take log and differentiate

`log f(t) = log t + 0.5 log (36-t^2)\\Y(t) = log t + 0.5 log (36-t^2)`

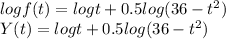
It is sufficient to find max or min of Y

`y'(t) = (1)/(t) -(t)/(36-t^2) \\\\y'=0 gives\\36-t^2 -t^2 =0\\t^2 =18\\t = 4.243,-4.243`

In the given interval only 4.243 lies

And we find this is maximum hence maximum at (4.243,18)

Minimum value is only when x = -1 i.e. -5.916

b)
`f(t) = 2cost +sin 2t\\f'(t) = -2sint +2cos2t\\f`

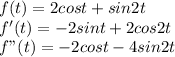
Equate I derivative to 0

-2sint +1-2sin^2 t=0

sint = 1/2 only satisfies I quadrant.

So when t = pi/6 we have maximum

Minimum is absolute mini in the interval i.e. (pi/2,0)