Question

PLEASE HELP 100PTS!!!!!!!! I SOLVED IT BUT I WANT TO CHECK MY ANSWERS!!

DONT COPY OTHER ANSWERS I CAN TELL AND REPORT YOU!!!!



A scientist is studying the growth of a particular species of plant. He writes the following equation to show the height of the plant f(n), in cm, after n days:


f(n) = 10(1.02)n


Part A: When the scientist concluded his study, the height of the plant was approximately 11.04 cm. What is a reasonable domain to plot the growth function?


Part B: What is the average rate of change of the function f(n) from n = 1 to n = 5, and what does it represent?

Answer 1

A) 0 ≤ n ≤ 5

B) 0.21 cm per day

Explanation:

Given:

`f(n)=10(1.02)^n`

where:

• f(n) = height of the plant (in cm)
• n = number of days

Part A

To find the upper limit of the domain, find when the height of the plant was approximately 11.04 cm by substituting f(n) = 11.04 and solving for n:

`\implies 10(1.02)^n=11.04`

`\implies (1.02)^n=(11.04)/(10)`

`\implies (1.02)^n=1.104`

`\implies \ln (1.02)^n= \ln 1.104`

`\implies n\ln 1.02= \ln 1.104`

`\implies n=( \ln 1.104)/(\ln 1.02)`

`\implies n=4.996304095...`

`\implies n=5`

Therefore, a suitable domain to plot the growth function is 0 ≤ n ≤ 5

Part B

The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:

`(f(b)-f(a))/(b-a)`

Therefore, the average rate of change of function f(n) over the interval 1 ≤ n ≤ 5 is:

`\implies (f(5)-f(1))/(5-1)`

`\implies (10(1.02)^5-10(1.02)^1)/(5-1)`

`\implies 0.210202008`

Therefore, the average rate of change is 0.21 cm per day.

This represents the average growth of the plant each day.

Answer 2

Part A) The reasonable domain to plot the growth function is the interval [0,5]

Part B) The average rate of change is
`0.21\ (cm)/(day)`

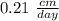
see the explanation

Explanation:

Part A)

Let

f(n) -----> the height of the plant in cm

n ----> the number of days

we have

`f(n)=10(1.02)^n`

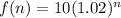
This is a exponential function of the form

`f(x)=a(b)^x`

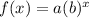
where

a is the initial value

b is the base

r is the rate of growth

b=(1+r)

In this problem we have

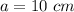`a=10\ cm` ----> initial value or y-intercept

`b=1.02`

`r=b-1=1.02-1=0.02`

`r=2\%`

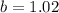
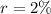
For f(n)=11.04 cm

Find the value of n

substitute in the exponential function

`11.04=10(1.02)^n`

`11.04/10=(1.02)^n`

`1.104=(1.02)^n`

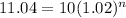
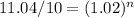
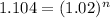
Apply log both sides

`log(1.104)=(n)log(1.02)`

`n=log(1.104)/log(1.02)`

`n=5\ days`

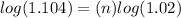
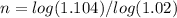
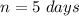
so

The reasonable domain to plot the growth function is the interval -----> [0,5]

`0 \leq x \leq 5`

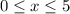
Part B) What is the average rate of change of the function f(n) from n = 1 to n = 5, and what does it represent?

the average rate of change is equal to

`(f(b)-f(a))/(b-a)`

In this problem we have

`f(a)=f(1)=10(1.02)^1=10.2\ cm`

`f(b)=f(5)=10(1.02)^5=11.04\ cm`

`a=1`

`b=5`

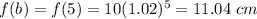
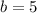
Substitute

`(11.04-10.2)/(5-1)=0.21\ (cm)/(day)`

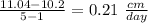
The average rate of change is the change of the function values (output values) divided by the change of the input values.

That represent ----> The plant grew an average of 0.21 cm per day during that time interval