Answer:
1327.43362 rev/s
Step-by-step explanation:
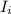 = Initial moment of inertia = 2.4 kgm² (arms outstretched)
= Initial moment of inertia = 2.4 kgm² (arms outstretched)
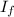 = Final moment of inertia = 0.904 kgm² (arms close)
= Final moment of inertia = 0.904 kgm² (arms close)
 = Final angular velocity
= Final angular velocity
 = Initial angular velocity = 0.5 rev/s
= Initial angular velocity = 0.5 rev/s
Here the angular momentum is conserved
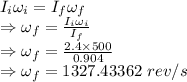
The new rate of rotation is 1327.43362 rev/s