Answer:
563712.04903 Pa
Step-by-step explanation:
m = Mass of material = 3.3 kg
r = Radius of sphere = 1.25 m
v = Volume of balloon =
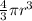
M = Molar mass of helium =
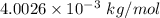
 = Density of surrounding air =
= Density of surrounding air =

R = Gas constant = 8.314 J/mol K
T = Temperature = 345 K
Weight of balloon + Weight of helium = Weight of air displaced
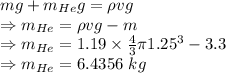
Mass of helium is 6.4356 kg
Moles of helium
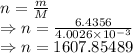
Ideal gas law

The absolute pressure of the Helium gas is 563712.04903 Pa