Answer:
The probabilities are:
- For no successful surgeries: practically 0
- For one successful surgery: 0.004
- For two successful surgeries: 0.021
- For three successful surgeries: 0.074
- For four successful surgeries: 0.167
- For five successful surgeries: 0.251
- For six successful surgeries: 0.251
- For seven successful surgeries: 0.161
- For eight successful surgeries: 0.06
- For nine successful surgeries: 0.01
Explanation:
Lets call X the total number of success. X counts the number of success from the same experiment repeated 9 times with a probability of success of 0.6 and one experiment independent of the other. Therefore X has Binomial distribution, X ≈ Bi(9,0.6).
The range of X is {0,1,2,3,4,5,6,7,8,9} and the probability of X being equal to a value k in its range is the number
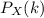 given by
given by
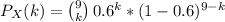
Thus,
I hope that works for you!