Answer: $645.50
Explanation:
The standard error of of the mean is given by :-
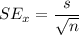 ,
,
where n= sample size .
s= sample standard deviation.
Given : You draw a random sample of 30 recent graduates and find that their average salary is $47,000, with a standard deviation of $5,000.
i.e. n= 60
Samples standard deviation : s= $5,000
Then, the standard error of the mean for this data will be :-
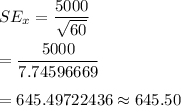 [To the nearest cent]
[To the nearest cent]
Hence, the estimate of the standard error of the mean for this data = $645.50