Question

Two rigid tanks of equal size and shape are filled with different gases. The tank on the left contains oxygen, and the tank on the right contains hydrogen. Assume both gases are ideal. The molar masses of oxygen and hydrogen are 32 and 2, respectively. Both containers are at the same temperature. A pressure gauge is pin oxygen hydrogen connected to each tank. Both gauges show a reading of 230 kPa.

Is the number of oxygen molecules in the left container greater than, less than, or equal to the number of hydrogen molecules in the right container? Explain your reasoning.

Answer 1

The number of oxygen molecules in the left container greater than the number of hydrogen molecules in the right container.

Step-by-step explanation:

Given:

Molar mass of oxygen,
`M_O=32`

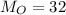
Molar mass of hydrogen,
`M_H=2`

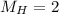
We know ideal gas law as:

`PV=nRT`

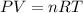
where:

P = pressure of the gas

V = volume of the gas

n= no. of moles of the gas molecules

R = universal gs constant

T = temperature of the gas

∵
`n=(m)/(M)`

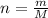
where:

m = mass of gas in grams

M = molecular mass of the gas

∴Eq. (1) can be written as:

`PV=(m)/(M).RT`

`P=(m)/(V).(RT)/(M)`

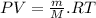
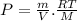
as:
`(m)/(V)=\rho\ (\rm density)`

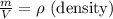
So,

`P=\rho.(RT)/(M)`

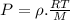
Now, according to given we have T,P,R same for both the gases.

`P_O=P_H`

`\rho_O.(RT)/(M_O)=\rho_H.(RT)/(M_H)`

`\Rightarrow (\rho_O)/(32)=(\rho_H)/(2)`

`\rho_O=16\rho_H`

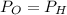
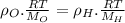
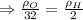
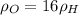
∴The molecules of oxygen are more densely packed than the molecules of hydrogen in the same volume at the same temperature and pressure. So, the number of oxygen molecules in the left container greater than the number of hydrogen molecules in the right container.