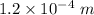Question

An aluminum cylinder with a radius of 2.7 cm and a height of 67 cm is used as one leg of a workbench. The workbench pushes down on the cylinder with a force of 3.2×104N. What is the compressive strain of the cylinder? Young's modulus for aluminum is 7.0×1010Pa. Express your answer using two significant figures. Compressive strain = nothing

By what distance does the cylinder's height decrease as a result of the forces on it?

Answer 1

`1.9* 10^(-4)`

`1.2* 10^(-4)\ m`

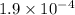
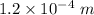
Step-by-step explanation:

r = Radius = 2.7 cm

F = Force =
`3.2* 10^4\ N`

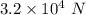
A = Area =
`\pi r^2`

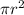
`\sigma` = Stress =
`(F)/(A)`

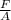
E = Young's modulus =
`7* 10^(10)\ Pa`

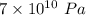
`\epsilon` = Strain

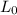`L_0` = Original length = 67 cm

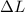`\Delta L` = Change in length

Young's modulus is given by

`E=(\sigma)/(\epsilon)\\\Rightarrow \epsilon=(\sigma)/(E)\\\Rightarrow \epsilon=((3.2* 10^4)/(\pi 0.027^2))/(7* 10^(10))\\\Rightarrow \epsilon=0.0001996=1.9* 10^(-4)`

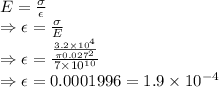
Strain is
`1.9* 10^(-4)`

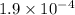
Strain is given by

`\epsilon=(\Delta L)/(L_0)\\\Rightarrow \Delta L=\epsilon* L_0\\\Rightarrow \Delta L=1.9* 10^(-4)* 0.67\\\Rightarrow \Delta L=0.0001273\\\Rightarrow \Delta L=1.2* 10^(-4)\ m`

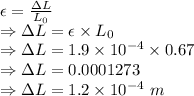
The cylinder height decreases by
`1.2* 10^(-4)\ m`