Question

What volume of nitrogen dioxide is formed at 735 torr and 28.2 °C by reacting 3.56 cm3 of copper (d = 8.95 g/cm3) with 200 mL of an aqueous solution of nitric acid (d = 1.42 g/ cm3, 68.0% by mass) ? Cu(s) + 4 HNO3 (aq) → Cu(NO3)2(aq) + 2NO2(g) + 2 H2O(ℓ)

Answer 1

25.76 L

Step-by-step explanation:

Given, Volume of Copper = 3.56 cm³

Density = 8.95 g/cm³

Considering the expression for density as:

`Density=\frac {Mass}{Volume}`

So,

So, Mass= Density * Volume = 8.95 g/cm³ * 3.56 cm³ = 31.862 g

Mass of copper = 31.862 g

Molar mass of copper = 63.546 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

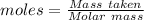
Thus,

`Moles= (31.862\ g)/(63.546\ g/mol)`

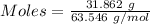
Moles of copper = 0.5014 moles

Given, Volume of nitric acid solution = 200 mL = 200 cm³

Density = 1.42 g/cm³

Considering the expression for density as:

`Density=\frac {Mass}{Volume}`

So,

So, Mass= Density * Volume = 1.42 g/cm³ * 200 cm³ = 284 g

Also, Nitric acid is 68.0 % by mass. So,

Mass of nitric acid =
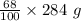`\frac {68}{100}* 284\ g` = 193.12 g

Molar mass of nitric acid = 63.01 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

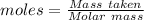
Thus,

`Moles= (193.12\ g)/(63.01\ g/mol)`

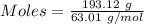
Moles of nitric acid = 3.0649 moles

According to the reaction,

`Cu_((s))+4HNO_3_((aq))\rightarrow Cu(NO_3)_2_((aq)) + 2NO_2_((g)) + 2H_2O_((l))`

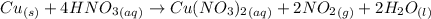
1 mole of copper react with 4 moles of nitric acid

Thus,

0.5014 moles of copper react with 4*0.5014 moles of nitric acid

Moles of nitric acid required = 2.0056 moles

Available moles of nitric acid = 3.0649 moles

Limiting reagent is the one which is present in small amount. Thus, nitric acid is present in large amount, copper is the limiting reagent.

The formation of the product is governed by the limiting reagent. So,

1 mole of copper on reaction forms 2 moles of nitrogen dioxide

So,

0.5014 mole of copper on reaction forms 2*0.5014 moles of nitrogen dioxide

Moles of nitrogen dioxide = 1.0028 moles

Given:

Pressure = 735 torr

The conversion of P(torr) to P(atm) is shown below:

`P(torr)=\frac {1}{760}* P(atm)`

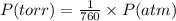
So,

Pressure = 735 / 760 atm = 0.9632 atm

Temperature = 28.2 °C

The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

T₁ = (28.2 + 273.15) K = 301.35 K

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

0.9632 atm × V = 1.0028 mol × 0.0821 L.atm/K.mol × 301.35 K

⇒V = 25.76 L