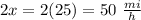Question

n a trip, a motorist drove 150 miles in the morning and 50 miles in the afternoon. His average rate in the morning was twice his average rate in the afternoon. He spent 5 hours driving. Find his average rate on each part of the trip.

Answer 1

Explanation:

A motorist drove 150 miles in the morning and 50 miles in the afternoon

His average rate in the morning was twice his average rate in the afternoon

He spent 5 hours driving

As=t*d

Cross multiply!!!

This is the equation

(750 - 150x = 100x =250x = 750 = x=3)

AS (Average speed is 50 mph

AS 25 mph

Hope it helps!

Answer 2

His average rate in the morning was
`50\ (mi)/(h)`

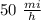
His average rate in the afternoon was
`25\ (mi)/(h)`

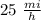
Explanation:

We need to remember the following formula:

`V=(d)/(t)`

Where "V" is the speed, "d" is the distance and "t" is the time.

Solving for "t":

`t=(d)/(V)`

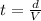
Let be
`x` the average rate in the afternoon and
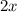`2x` the average rate in the morning.

Since he spent 5 hours driving, we can write the following equations:

`5=(150)/(2x)+(50)/(x)`

Solving for "x", we get:

`5=(150)/(2x)+(50)/(x)\\\\5=(75+50)/(x)\\\\5x=125\\\\x=(125)/(5)\\\\x=25`

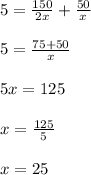
Therefore, his average rate in the afternoon was:

`x=25\ (mi)/(h)`

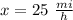
And his average rate in the morning was:

`2x=2(25)=50\ (mi)/(h)`