Question

A baseball is thrown in a parabolic arc. Help?

Answer 1

The maximum height of the baseball is 9 feet

Explanation:

we have

`p(t)=(1)/(2)gt^2+v_0t+p_0`

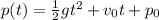
where

p(t) ----> baseball position above the ground in feet

t ----> the time in seconds

v_0 ----> is the initial velocity in ft/sec

p_0 ---> initial position above the ground

we have

`g=-32(ft)/(sec^2) \\\\v_0=16(ft)/(sec)\\\\p_0=5\ ft`

substitute the given values

`p(t)=(1)/(2)(-32)t^2+16t+5`

`p(t)=-16t^2+16t+5`

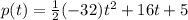
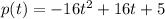
This is the equation of a vertical parabola open downward

The vertex represent a maximum

Convert the quadratic equation in vertex form

`p(t)=-16t^2+16t+5`

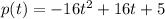
Factor -16 leading coefficient

`p(t)=-16(t^2-t)+5`

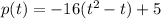
Complete the square

`p(t)=-16(t^2-t+(1)/(4))+5+4`

`p(t)=-16(t^2-t+(1)/(4))+9`

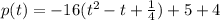
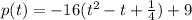
Rewrite as perfect squares

`p(t)=-16(t-(1)/(2))^2+9`

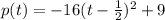
The vertex is the point (0.5,9)

The maximum height of the baseball above the ground is the y-coordinate of the vertex

therefore

The maximum height of the baseball is 9 feet