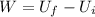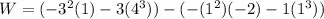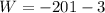Answer:
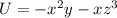
since the work done in closed path for above function is independent of the path so this is a conservative field

Step-by-step explanation:
As we know that
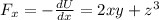
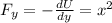

now from above 3 equations we have
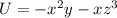
since the work done in closed path for above function is independent of the path
so this is a conservative field
Now work done in moving the object is given as