Answer:
The slope-intercept form of both equations is
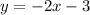 .
.
Explanation:
The given system of equations is
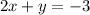
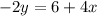
The slope-intercept form of an equation is

where, m is slope and b is y-intercept.
We need to write each equation in slope-intercept form.
First equation is
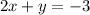 (Given)
(Given)
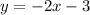 (Subtract 2x on both sides)
(Subtract 2x on both sides)
The slope-intercept form of first equation is
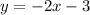 .
.
Second equation is
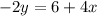 (Given)
(Given)
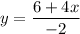 (Divide both sides by -2)
(Divide both sides by -2)
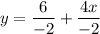
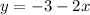
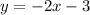
The slope-intercept form of first equation is
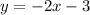 .
.
Both equation have same slope intercept form it means both lines coincide each other.
So, the given system of equation have infinitely many solutions.