Question

Abook contains 400 pages. If their are 80 typing errors randomly distributed throughout the book,use the Poisson distribution to determine the probability that a page contains exactly 2 errors.

Answer 1

using the Poisson distribution to determine the probability that a page contains exactly 2 errors is 0.0163

Solution:

Given that, A book contains 400 pages.

There are 80 typing errors randomly distributed throughout the book,

We have to use the Poisson distribution to determine the probability that a page contains exactly 2 errors

The poisson distribution is given as:

`\text { Poisson distribution }=e^(-\lambda) (\lambda^(k))/(k !)`

`\begin{array}{l}{\text { Where, } \lambda \text { is event rate of distribution for observing k events. }} \\\\ {\text { Here rate of distribution } \lambda=\frac{\text { 80 mistakes }}{400 \text { pages }}=(1)/(5)}\end{array}`

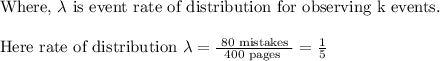
And, k = 2 errors.

Plugging in values in poisson distribution, we get

`\begin{array}{l}{\mathrm{p}(2)=e^{-(1)/(5)} * ((1)/(5)^(2))/(2 !)} \\\\ {=2.7^{-(1)/(5)} * ((1)/(5^(2)))/(2 * 1)}\end{array}`

On solving, we get

= 0.0163

Hence, the probability is 0.0163.