To solve this problem it is necessary to apply the concepts related to linear momentum, velocity and relative distance.
By definition we know that the relative velocity of an object with reference to the Light, is defined by
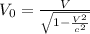
Where,
V = Speed from relative point
c = Speed of light
On the other hand we have that the linear momentum is defined as
P = mv
Replacing the relative velocity equation here we have to
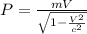
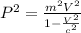
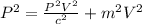
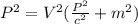
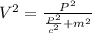


Therefore the height with respect the observer is

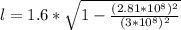
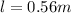
Therefore the height which the observerd measure for her is 0.56m