Question

The following hypotheses are given. H0 : σ1² ≤ σ2² H1 : σ1² > σ2² A random sample of five observations from the first population resulted in a standard deviation of 12. A random sample of seven observations from the second population showed a standard deviation of 7. At the 0.01 significance level, is there more variation in the first population?

Answer 1

Desision is to not reject the null hypothesis, this means that the variance of the second population is equal or greater than the variance of the first population.

Explanation:

Hello!

You have the hypothesis set:

H₀: δ₁² ≤ δ₂²

H₁: δ₁² > δ₂²

α: 0.01

To study the population variance of two populations you have to work with the F-distribution. The statistic is:

F= (S₁²/S₂²)*(σ₁²/σ₂²) ~ F
`_((n1-1);(n2-1))`

This is a one tailed test, the critical value is

`F_((n1-1); (n2-1); 1-\alpha ) = F_(4; 6; 0.99) = 9.15`

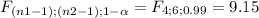
If the statistic value F
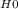`_(H0)` ≥ 9.15, the decision is to reject the null hypothesis.

If the value F
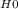`_(H0)` < 9.15, the decision is to not reject the null hypothesis.

F
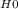`_(H0)`= (S₁²/S₂²)*(σ₁²/σ₂²) = (12/7) * 1

F
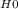`_(H0)`= 1.714

Desision is to not reject the null hypothesis, this means that the variance of the second population is equal or greater than the variance of the first population.

I hope you have a SUPER day!