Question

At what point will 3y=4x-6 and 8x-6y=-30 intercept

Answer 1

The lines don't intercept

Explanation:

we have

`3y=4x-6`

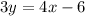
isolate the variable y

Divide by 3 both sides

`y=(4)/(3)x-(6)/(3)`

simplify

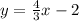`y=(4)/(3)x-2` -----> equation A

`8x-6y=-30`

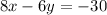
Isolate the variable y

`6y=8x+30`

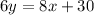
Divide by 6 both sides

`y=(8)/(6)x-(30)/(6)`

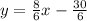
simplify

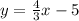`y=(4)/(3)x-5` -----> equation B

Compare equation A and equation B

The slopes are the same and the y-intercepts are different

Remember that

If two lines has the same slope, then the lines are parallel

therefore

In this problem line A and line B are parallel lines

The system of equations has no solution, because the lines don't intercept