Answer:
b. about 63.9 units and 41.0 units
Explanation:
In question ∠a= 29° and Side of a= 15 and b= 20
Using sine rule of congruence of triangle.
⇒
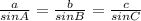
⇒
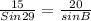
Using value of sin 29°
⇒
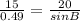
Cross multiplying both side.
⇒ Sin B=
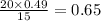
∴ B= 41°
Now, we have the degree for ∠B= 41°.
Next, lets find the ∠C
∵ we know the sum total of angle of triangle is 180°
∴∠A+∠B+∠C= 180°
⇒
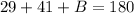
subtracting both side by 70°
∴∠C= 110°
Now, again using the sine rule to find the side of c.
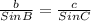
⇒
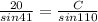
Using the value of sine and cross multiplying both side.
⇒ C=
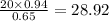
∴ Side C= 28.92.
Now, finding perimeter of angle of triangle
Perimeter of triangle= a+b+c
Perimeter of triangle=
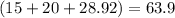
∴ Perimeter of triangle= 63.9 units