Question

Find the perimeter of each of the two non congruent triangles where a=15,b=20 and a=29

a. about 54.6 units and 39.4 units


c. about 46.8 units n 64.6 units


b. about 63.9 units and 41.0 units


d. about 67.5 units and 36.8 units please select the best answer from the choices provided

Answer 1

b. about 63.9 units and 41.0 units

Explanation:

In question ∠a= 29° and Side of a= 15 and b= 20

Using sine rule of congruence of triangle.

⇒
`(a)/(sin A) = (b)/(sin B) = (c)/(sin C)`

⇒
`(15)/(Sin 29) = (20)/(sin B)`

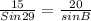
Using value of sin 29°

⇒
`(15)/(0.49) = (20)/(sin B)`

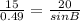
Cross multiplying both side.

⇒ Sin B=
`(20* 0.49)/(15) = 0.65`

∴ B= 41°

Now, we have the degree for ∠B= 41°.

Next, lets find the ∠C

∵ we know the sum total of angle of triangle is 180°

∴∠A+∠B+∠C= 180°

⇒
`29+41+B= 180`

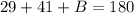
subtracting both side by 70°

∴∠C= 110°

Now, again using the sine rule to find the side of c.

`(b)/(SinB) = (c)/(SinC)`

⇒
`(20)/(sin41) = (C)/(sin110)`

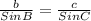
Using the value of sine and cross multiplying both side.

⇒ C=
`(20* 0.94)/(0.65) = 28.92`

∴ Side C= 28.92.

Now, finding perimeter of angle of triangle

Perimeter of triangle= a+b+c

Perimeter of triangle=
`(15+20+28.92)= 63.9`

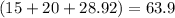
∴ Perimeter of triangle= 63.9 units