Answer:
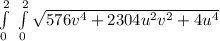 du dv
du dv
Explanation:
let, r = x i + y j + z k , where i, j, k are unit vectors.
r =
 i + uv j + 12
i + uv j + 12
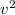 k
k
we know that the surface area of a surface represented by r(u,v) is
=
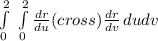
here,
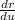 = 2u i + v j
= 2u i + v j
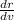 = u j + 24 v k
= u j + 24 v k
Cross product =
![\left[\begin{array}{ccc}i&j&k\\2u&v&0\\0&u&24v\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/umruhpta9c6w47brn9gv4nx0zbb64wsa1p.png)
= 24
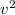 i - 48 uv j + 2
i - 48 uv j + 2
 k
k
The modulus of the cross product is

so, the surface area is
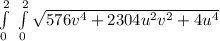 du dv
du dv
and the answer has to be left as the integral itself as the integral of square root of biquadratic can not be calculated(with random co efficients).