Question

A cylindrical specimen of some metal alloy 11.1 mm (0.4370 in.) in diameter is stressed elastically in tension. A force of 14000 N (3147 lbf) produces a reduction in specimen diameter of 7 × 10-3 mm (2.756 × 10-4 in.). Compute Poisson's ratio for this material if its elastic modulus is 100 GPa (14.5 × 106 psi).

Answer 1

To develop this problem it is necessary to apply the concepts related to the uni-axial deflection of bodies.

From the expression of Hooke's law we have to

`\sigma = E\epsilon`

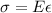
Where,

E= Young's modulus

`\epsilon =` The strain

And substituting P/A for stress and
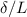`\delta/L` for strain gives that

`(P)/(A) = E(\delta)/(L)`

Where,

P = Force

A = Area

L = Length

Therefore this can be re-arranged to give

`\delta = (PL)/(AE)`

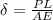
If we want to calculate the deformation per unit area then we can also rewrite the equation as

`(delta)/(L) = (P)/(AE)`

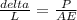
Replacing with our values we have to

`(delta)/(L) = (14400)/((\pi/4 (11.1*10^(-3))^2)(100*10^9))`

`(delta)/(L) = 0.001488`

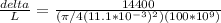
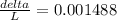
Therefore the posion ratio would be

`\upsilon = ((\delta_(decreased))/(d))/((\delta_l)/(L))`

`\upsilon = ((7*10^(-3))/(11.1))/(0.001488)`

`\upsilon = 0.4238`

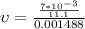
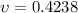
Therefore the Poisson's ratio for this material is 0.4238