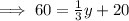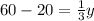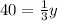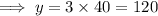Question

Given that ΔABC ≅ ΔDEF, m∠A = 70°, m∠B = 60°, m∠C = 50°,m∠D = (3x + 10)°, m∠E= (1/3y + 20)°, and m∠F = (z2 + 14)°, find the values of x and y.

Answer 1

Value of x is 20 and y is 120.

Explanation:

Given,

m∠A = 70°, m∠B = 60°, m∠C = 50°,m∠D = (3x + 10)°, m∠E= (1/3y + 20)°, and m∠F = (z² + 14)°

Also,

ΔABC ≅ ΔDEF,

Since, the corresponding parts of congruent triangles are always congruent or equal.

⇒ m∠A = m∠D, m∠B = m∠E and m∠C = m∠F

When m∠A = m∠D

`\implies 70 = 3x + 10`

`70 - 10 = 3x`

`60 = 3x`

`\implies x =(60)/(3)=20`

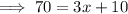
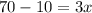
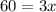
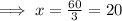
When, m∠B = m∠E,

`\implies 60 = (1)/(3)y + 20`

`60 - 20 =(1)/(3)y`

`40 =(1)/(3)y`

`\implies y =3* 40=120`