Question

Lily swims for 5 hours in stream that has a current of 1 mph. She leaves her dock, swims upstream for 2 miles and then swim back to her dock. What is her swimming speed in still water?

Answer 1

Swimming speed in still water is approximately 1.5 mph

Explanation:

Given the speed of the current = 1 mph

distance she swims upstream =2 miles,

the total time = 5 hours.

She swam 2 miles upstream against the current and 2 miles back to the dock with the current. The formula that relates distance, time, and rate is
`d = r t\ \ \ \ or  \ \ \  t= (d)/(r)`

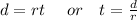
Let x be the speed in still water.

Then her speed with the current is x + 1, and

her speed against the current is x – 1.

Total time is equal to 2 miles with upstream and 2 miles downstream.

`(2)/(x+1)+(2)/(x-1)=5\\\\(2(x-1))/((x+1)(x-1))+(2(x+1))/((x-1)(x+1))=5\\\\(2x-2)/((x^2-1))+(2x+2))/((x^2-1))=5\\\\(2x-2+2x+2))/((x^2-1))=5\\\\4x=5(x^2-1)\\4x= 5x^2-5\\0= 5x^2-4x-5`

Now Using quadratic formula to solve above equation we get;

`x= \frac{-b \±√(b^2-4ac)} {2a}\\\\here \ \ a= 5,b=-4,c=-5\\\\x= \frac{-(-4) \±√((-4)^2-4* 5*-5)} {2*5}\\\\x=\frac{4 \±√(16+100)} {10}\\\\x=\frac{4 \±√(116)} {10}=x=\frac{4 \±2√(29)} {10}= x=\frac{2 \±√(29)} {5}\\ x \approx 1.5 \ or \ x = -0.7`

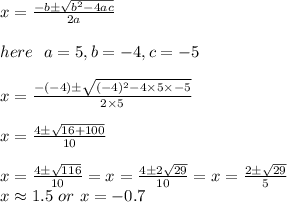
Since speed must be positive, Hence speed of still water is about 1.5 miles per hour.