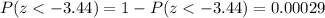Answer:
a)
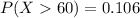
b)

c)
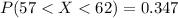
d)
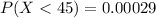
Explanation:
1) Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Let X the random variable that represent the gas mileage for a hybrid car of a population, and for this case we know the distribution for X is given by:
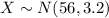
Where
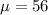 and
and
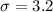
(a) What proportion of hybrids gets over 60 miles per gallon?
We are interested on this probability
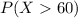
And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
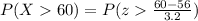
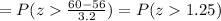
And we can find this probability on this way:
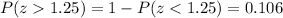
(b) What proportion of hybrids gets 52 miles per gallon or less?
We are interested on this probability

And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
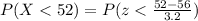

And we can find this probability on this way:
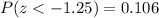
(c )What proportion of hybrids gets between 57 and 62 miles per gallon?
We are interested on this probability
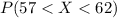
And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
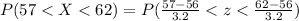
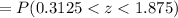
And we can find this probability on this way:
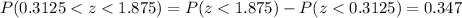
(d) What is the probability that a randomly selected hybrid gets less than 45 miles per gallon?
We are interested on this probability
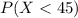
And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
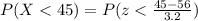
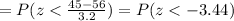
And we can find this probability on this way: